Notches and Weirs- Their classification and types

Notch- is a device used for measuring the rate of flow or discharge of a liquid through  small channel or tank.
Weir- is a concrete or masonry structure, placed in an open channel over which the flow occurs.
It is form of vertical wall , with the sharp edge at the top, running all the way across the open channel.

Notches	Weirs
1. A notch may be defined as an opening provided in one side of a tank or reservoir,with upstream liquid level below the top edge of opening.	1. A weir may be defined as a structure constructed across a river or canal to store water on the upstream side.
2. The sheet of water flowing through a notch is called Nappe.	2. The sheet of water flowing over a weir is called Vein.
3. The bottom edge of a notch is called Crest.	3. The bottom edge of a weir is called Sill.
4. Usually made of metallic plates.	4. Weir is a concrete or masonry structure
5. Measures small discharge of small stream, lake or canal.	5. It can measure large discharge of rivers and canals.
6. Notches are of small size.	6. Weirs are of bigger size.

Notch

Weir

Classification of Notches and Weirs

Notches are classified as:

1. According to the shape of opening

a) Rectangular notch
b) Triangular notch
c) Trapezoidal notch
d) Stepped notch

2. According to the effect of the sides on the nappe
a) Notch with end contraction
b) Notch without end contraction or suppressed notch

Weir are classified according to the shape of the opening, the shape of the crest ,the effect of the sides on the nappe and the nature of discharge
a) According to the shape of the opening:
 1. Rectangular weir
 2. Triangular weir
 3. Trapezoidal weir

b) According to the shape of the crest
 1. Sharp-crested weir
 2. Broad-crested weir
 3. Narrow-crested weir
 4. Ogee-shaped weir

c) according to the effect of the sides on the emerging nappe
 1. weir with end contraction
 2.  weir without end contraction

Discharge over a Rectangular Notch or Weir

The expression for discharge for Rectangular Notch or Weir is same

Consider a Rectangular Notch or Weir provided in a channel carrying water as shown in fig

Let  H =Head of water over the crest

        L=Length of Rectangular Notch or Weir

For finding the discharge of water flowing over the Notch or Weir ,consider an elementary horizontal strip of water of thickness dh and length L at a depth h from free surface of water

The area of strip=L*dh

And theoretical velocity of water flowing through the strip =√2gh

The discharge dQ through the strip is given by

dQ=Cd* area of strip *Theoretical velocity

=Cd*L*dh*√2gh

Cd = Coefficient of discharge

The total discharge Q is given by integrating dQ between 0 to H

Q= 2/3* Cd * √2g* L* H ^1.5

Discharge over a Triangular Notch or Weir

The expression for discharge over a triangular Notch or Weir is same

Let H= Head of water above V notch

Theta = angle of notch

Q= 8/15* Cd* √ 2g*tan θ/2 * H៱5/2

Advantages of triangular Notch or Weir over Rectangular Notch or Weir

A triangular notch or weir is preferred over a rectangular notch or weir due to following reasons

1. The expression for discharge for a right angled V notch or weir is very simple.

2.For measuring low discharge ,a triangular notch gives more accurate results than a rectangular notch.

3. In case of triangular notch ,only one reading  ie. H is required for the computation of discharge.

4. Ventilation of triangular notch is not necessary.

Discharge over a Trapezoidal notch or Weir

Trapezoidal notch is a combination of rectangular and triangular notch. Thus the total discharge will be sum of discharge through rectangular notch or weir and triangular notch or weir.

Let  H =Head of water over the crest

        L=Length of the crest of the  Notch

Cd1= Coefficient of discharge for rectangular portion

Cd2= Coefficient of discharge for triangular portion

Q1=2/3* Cd * √2g* L* H ^1.5

Q2=8/15* Cd2* √2g* tan θ/2 * H៱5/2

Discharge through trapezoidal notch or weir=Q1+Q2

Q=2/3* Cd * √2g* L* H ^1.5 + 8/15* Cd2* √2g* tan θ/2 * H៱5/2

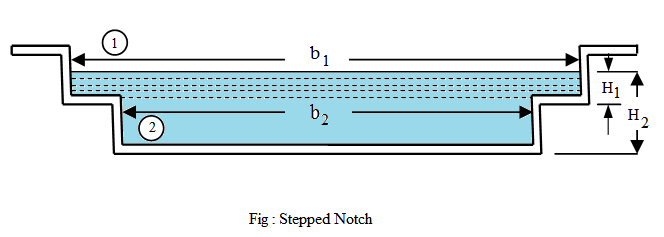
Discharge over a Stepped Notch

A stepped notch is a combination of rectangular notches. The discharge through the stepped notch is equal to the sum of the discharges through the different rectangular notch

Q=2/3* Cd * √2g* b2* (H2^1.5-H1^1.5 ) + 2/3* Cd * √2g* b1* H1^1.5

Effect of Discharge over a Notch or Weir due to error in the measurement of head

• For rectangular notch

Q=2/3* Cd * √2g* L* H ^3/2

Q=K*H^3/2 where  K= 2/3* Cd * √2g* L

Differentiating the above equation we get

dQ= K*1.5 H ½
dividing dq by Q 

dQ/Q= 1.5 dH/H

this tells that an error of 1% in measuring H will produce 1.5% error in Discharge

• For triangular notch

Q= 8/15* Cd2* √2g* tan θ/2 * H៱5/2

Q=K*H^5/2 where K= 8/15* Cd2* √2g* tan θ/2

Differentiating the above equation we get

dQ= K*2.5 H3/2
dividing dq by Q 

dQ/Q= 2.5 dH/H

this tells that an error of 1% in measuring H will produce 2.5% error in Discharge

Time required to empty a reservoir or a tank with a rectangular notch or weir

T=3A/(Cd L root 2g)*(1/H2 -1/H1)

Time required to empty a reservoir or a tank with a triangular notch or weir

T=5A/(4 Cd tan /2 root 2g)*(1/H2 -1/H1)

Velocity of approach

Velocity of approach is defined as the velocity with which the water approaches or reaches the weir or notch before it flows over it. Thus if Va is the velocity of approach then an additional head ha equal to Va2/2g due to  velocity of approach, is acting on the water flowing over the notch. Then initial height of water over the notch becomes (H + ha) and final height becomes ha.

Then all the formula are changed taking into consideration of velocity of approach.

Va=Q/Area of channel

Empirical Formula  for discharge over rectangular weir

Q=2/3 *Cd *√2g *L *[(H + ha)៱3/2 –ha ៱3/2]

Francis formula:He considered that the end contraction decreases the effective length of the crest of weir and hence decrease the discharge. Each end contraction reduces the crest length by 0.1*H, where H is the head over the weir. For a rectangular weir having two end contraction only hence effective length is:

L=( L- 0.2*H)

                                                          Q=2/3 *Cd *√2g *( L- 0.2*H) * H៱3/2

if Cd=0.623  g=9.81 m/s៱2 then 

after simplifying

Q=1.84*( L- 0.2*H)* H៱3/2

If  end contraction are suppressed ,then 

Q=1.84* L* H៱3/2

If Velocity of approach is considered ,then

Q=1.84*L *[(H + ha)៱3/2 –ha ៱3/2]

Bazin formula:  He proposed that 

Q=m  *L *√2g *H៱3/2

                                                      where m=2/3*Cd=0.405+0.003/H 

Cipolletti Weir or notch

A standard Cipolletti weir is trapezoidal in shape  The crest and sides of the weir plate are placed far enough from the bottom and sides of the approach channel to produce full contraction. The sides incline outwardly at a slope of 1 horizontal to 4 vertical.

tan θ/2=1/4

by giving this slope to the sides, an increase in discharge through the triangular portion ABC and DEF of the weir is obtained. If this slope is not provided the weir would be rectangular one, and due to end contraction,the discharge would decrease.

                                               Q=2/3 *Cd *√2g *( L- 0.2*H) * H៱3/2

                                         Q=2/3 *Cd *√2g * L *H៱3/2- 2/15* Cd * √2g * H៱5/2

due to end contraction the discharge decreases by 2/15* Cd * √2g * H៱5/2. This decrease in discharge can be compensated by giving such a slope that the discharge through two triangular portions i equal to 2/15* Cd * √2g * H៱5/2. On equating this decrease with the triangular notch discharge 

2/15* Cd * √2g * H៱5/2= 8/15* Cd* √ 2g*tan θ/2 * H៱5/2

on solving we will get

tan θ/2=1/4

Thus discharge through Cipolletti weir is

Q=2/3 *Cd *√2g * L *H៱3/2

Discharge over a OGEE Weir

it is similar to rectangular weir hence

                                                       Q=2/3 *Cd *√2g * L *H៱3/2

That's for all for this blog

                                              Thanks for reading till now

            stay in your home to fight against COVID-19

                                    Stay tuned ...

                                         :)